这里有一个其他人做的讲解视频.
翻译自 How Planimeters Work, 作者 Robert Foote. 翻译时有改动.
原文最后更新于 2009/5/26.
本文中的优雅证明主要来自 O.Henrici 的这篇论文:
O. Henrici, Report on Planimeters, British Assoc. for the Advancement of Science, Report of the 64th meeting, 1894, pp. 496-523.
其中还包含了一些关于求积仪的有意思的历史, 一直到 1894 年.
我喜欢这个证明的原因有下面几点: 它几乎是纯几何证明, 没有用到复杂的代数, 而且不需要用到微积分就可以直观地解释. 此外, 它还说明了线性和极坐标求积仪虽然有相似的结构, 但工作原理不尽相同. 因此, 这个解释也适用于这两种求积仪的变体, 包括用于证明等周不等式.
线动成面
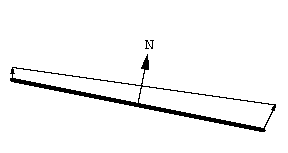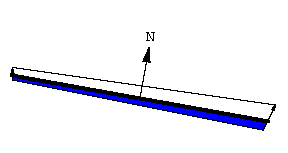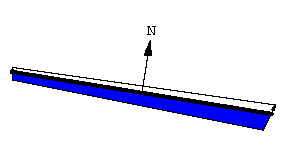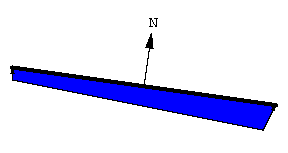
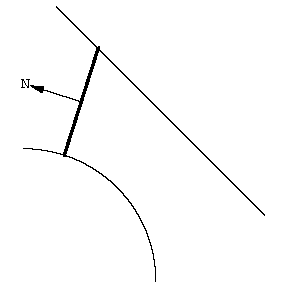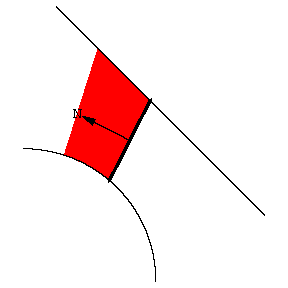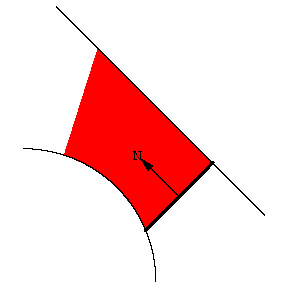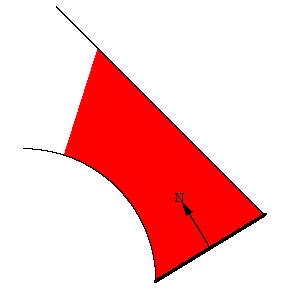
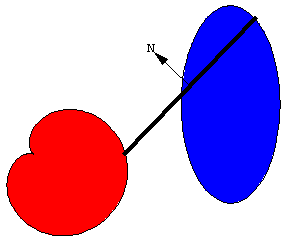
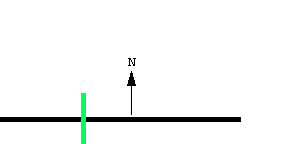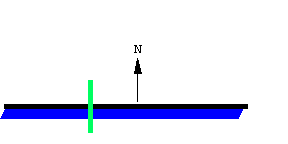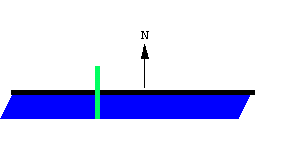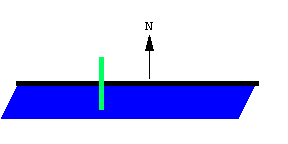
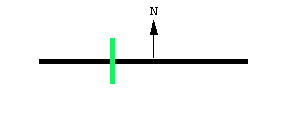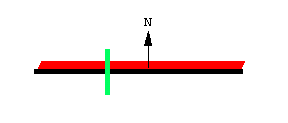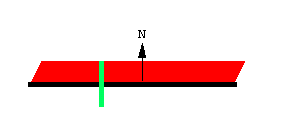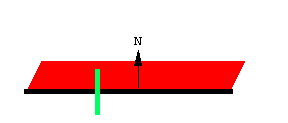
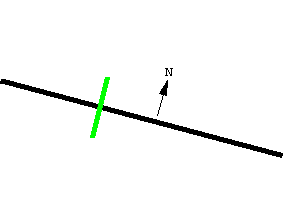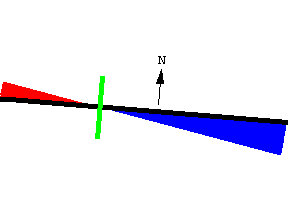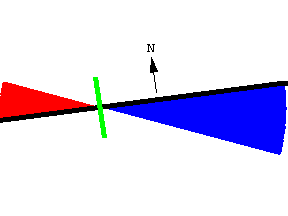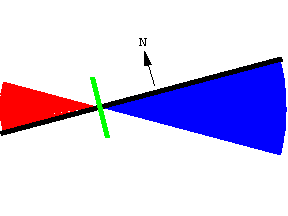
求积仪的原理基于一个直观概念: 线动成面. 这条线段扫出了一个窄四边形. 线段的朝向由向量 \bold N 决定, \bold N 是线段的法向量, 也就是与线段垂直的向量.
扫过的面积是有符号的, 或者说有朝向的. \bold N 指向正方向.
沿 \bold N 方向扫过的面积为正.
沿 \bold N 的反方向扫过的面积为负.
积差定理
设两动点沿两条封闭曲线逆时针移动, 这两点构成一条有朝向线段. 线动定理告诉我们, 线段扫过的有符号面积等于曲线所围成的面积之差, 即
\colorbox{lightyellow}{$ A = A_R - A_L $}其中 A_L 和 A_R 分别为线段的左右端点所在曲线的面积.
把移动线段变成求积仪
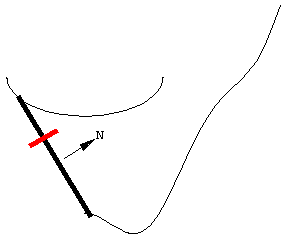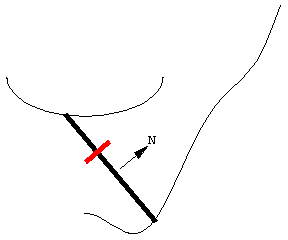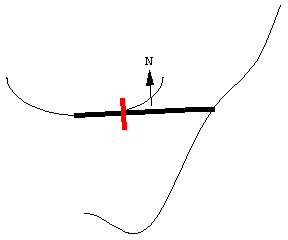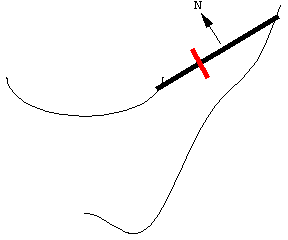
把移动线段变成求积仪, 只需要让长度固定, 再加上一个滚轮 (红色部分). 滚轴平行于线段. 在极坐标和线性求积仪的原理图上, 以及在我的 K&E 极坐标求积仪的托架底面, 都可以明显看到滚轮. 我们可以得出一个惊人的结论: 当极坐标或线性求积仪被用于沿一个区域的边界移动时, 滚轮的滚动量与该区域的面积成正比. 理由会在下文解释.
图中展示了一个移动的求积仪, 其两端沿着两条曲线运动. 尽管曲线不同, 求积仪的长度并不会改变.
随着求积仪移动, 滚轮部分滚动, 部分滑动. 线段沿向量 \bold N 方向的运动导致滚轮滚动, 并被记录在与滚轮连接的刻度盘上. 线段沿其长度方向的运动导致滚轮滑动, 并不会被记录. 因此, 滚轮记录的是垂直于求积仪长度方向上的运动分量.
向量 \bold N 指示的方向是扫过的面积为正值的方向——并不一定是运动的方向. 注意这个动画的细节: 为了沿曲线运动, 求积仪的左端不得不在某一点上反向移动.
滚动与面积的关系
求积仪的运动有两种基本类型.
第一种类型的运动是求积仪平行于自身的运动, 此时它扫过的部分是一个平行四边形. 有一个重要事实需要注意: 滚轮滚动的距离, 正好是平行四边形的高, 因为滚轮记录了垂直于连杆方向上的运动. 如果 A 表示扫过的面积, s 表示滚轮的滚动距离, 我们可以得到
A = ls其中 l 是求积仪的长度, 也就是平行四边形的宽. 注意, 如果求积仪的运动方向与 \bold N 相反, 滚轮会向后滚动. 上述方程仍然有效, 但 A 和 s 都是负值.
第二种类型的运动是求积仪绕滚轮旋转. 此时, 扫过的面积部分为正, 部分为负. 还需注意, 滚轮并没有滚动. 在这种情况下, 扫过的净面积与求积仪旋转的角度和滚轮的位置有关. 联系这些量的公式是
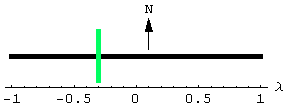
A = - \frac{1}{2} l^\prime l^2 \theta这需要稍作解释. 滚轮可以位于连杆上的任何一点. 量 l^\prime 在 -1 和 1 之间, 表示滚轮在连杆上的位置. 滚轮在右端点时, l^\prime = 1; 在左端点时, l^\prime = -1; 在中点时, l^\prime = 0. 在图示例子中, l^\prime = - \frac{3}{10}.
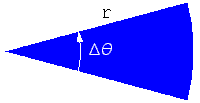
想要求出扫过的有符号面积, 首先要回忆一下, 扇形的面积是 A = \frac{1}{2} r^2 \theta.
如果 A 与 l^\prime 线性相关对你是显然的, 可以注意到 A = - \frac{1}{2} l^\prime l^2 \theta 一定是正确的公式, 因为它给出了 l^\prime=-1, 0, 1 时的正确有符号面积. 如果不够显然, 这里有更完整的推导.
一般地, 求积仪的运动是平移和旋转的组合. 扫过的有符号面积简单地等于平移和旋转部分之和.
\colorbox{lightyellow}{$ A = ls - \frac{1}{2} l^\prime l^2 \theta $}结合线动定理和滚轮滚动
现在, 假设求积仪的连杆移动一周, 并最终静止在开始时的同一位置. 那么上面两个关于有符号面积的公式 (黄色框内) 都是有效的, 因此我们得到
\colorbox{lightgreen}{$ A_R - A_L = ls - \frac 1 2 l^\prime l^2 \theta $}此外, \theta 是 2 \pi 的整数倍, 一般为 0 或 2 \pi.
测量一个区域
当使用求积仪测量一个区域时, 使用者在待测区域的边界上移动连杆的右端点, 即追踪点. 因此, 所求的区域是 A_R. 对于线性求积仪来说, 左端点沿直线来回运动, 没有围住任何面积, 因此 A_L = 0. 同样, 对于以通常方式使用的极坐标求积仪来说, 左端点沿圆弧运动, 但没有完整地绕圆一周, 同样 A_L = 0. 对于以通常方式使用的这两种求积仪来说, 连杆都不会完整地旋转, 因此 \theta = 0. 将这些代入到上方绿框中的公式, 就可以得到所测区域面积的简单公式
A_R = ls由此可以观察到三个简单事实.
- 该区域的面积与滚轮的滚动量成正比. 比例系数是求积仪连杆的长度. 与滚轮相连的刻度盘在设计之出就考虑到了这一点, 使用者可以直接从刻度上读出量
ls. - 滚轮在连杆的位置并不重要.
- 左端点可以沿任何不闭合面积的路径移动——极坐标和线性求积仪只是特殊情况.
极坐标求积仪可以用来测量一个大的区域, 只需要把它的极点放在待测区域内。(极点是极臂的固定端点--也是描边臂左端点所绕的圆的圆心.) 当以这种方式使用时, 左端点完整地绕了它所跟随的圆一周, 因此 A_L = \pi r^2, 其中 r 是这个圆的半径, 即极臂的长度. 此外, 示踪臂完整地旋转了一周, 所以 \theta = 2 \pi. 将这些代入到上面绿框内的公式中,可以得到
A_R = ls + \pi r^2 - l^\prime \pi l^2为待测区域的面积. 使用者从刻度上读出量 ls, 然后加上 \pi r^2 - l^\prime \pi l^2, 得到所求面积. 额外加上的量涉及到求积仪两臂的长度和滚轮的位置. 这些都是仪器的常数, 一般印在说明书上.

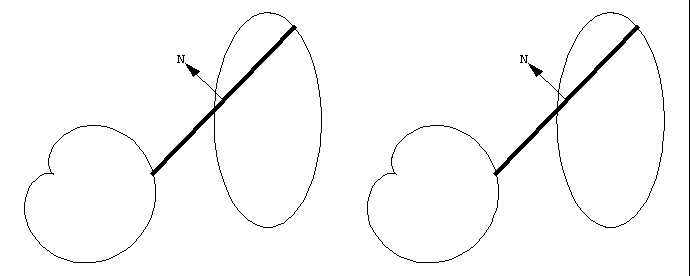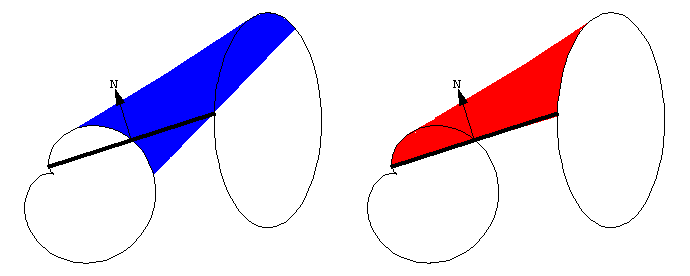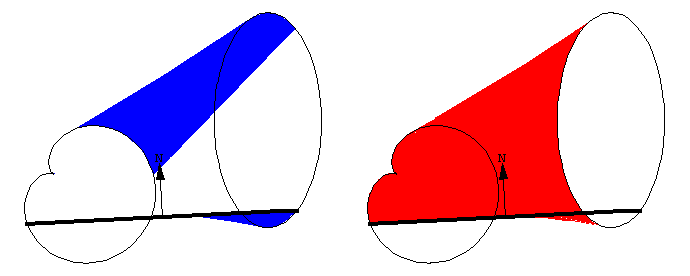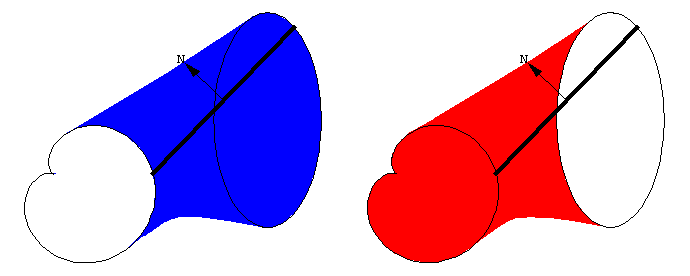

文章评论
非常感谢大佬!
ヘ⌒ヽフ
( ・ω・) 谢谢~~
/ ~つと)